


리트코드 - 212. Word Search II
출처 - https://leetcode.com/problems/word-search-ii/?envType=study-plan-v2&envId=top-interview-150
문제 설명
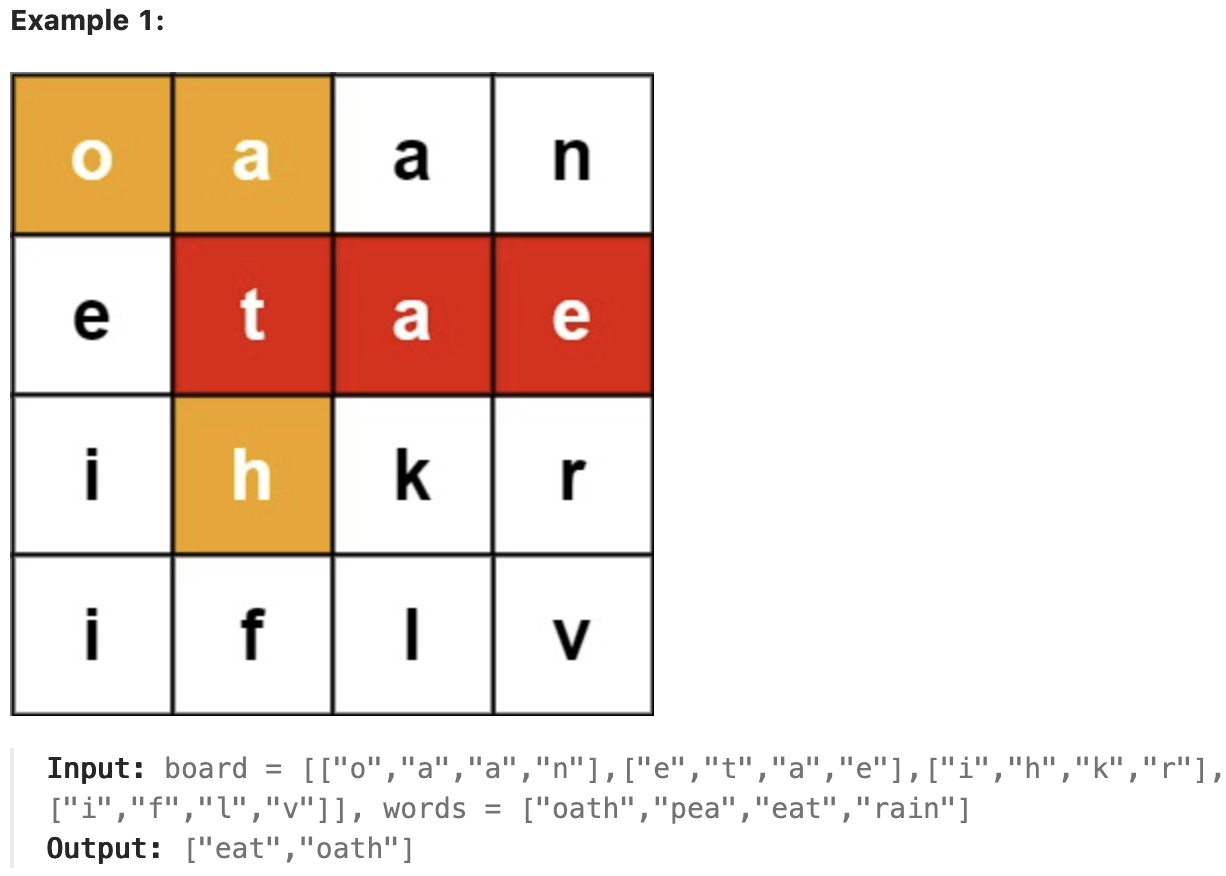
주어진 m x n 문자열 보드와 문자열 목록 words가 있을 때, 보드에서 찾을 수 있는 모든 단어를 반환합니다. 각 단어는 인접한 셀의 문자로 구성되어야 하며, 인접한 셀은 가로 또는 세로로 이웃한 셀을 의미합니다. 동일한 문자 셀은 한 단어 내에서 두 번 이상 사용할 수 없습니다.

의사코드
| class Node Node배열 children boolean isEndOfWord 생성자 children = new Node[26] isEndOfWord = false class Trie Node root 생성자 root = new Node insert 메소드(word) 현재Node = this.root 반복문 시작 (word의 각 문자 하나씩) idx = c - 'a' if (현재Node의 children[idx] == null) 현재Node의 children[idx] = new Node 현재Node = 현재Node의 children[idx] 반복문 종료 현재Node의 isEndOfWord를 true로 설정 class Solution 함수 findWords(board, words) answer 리스트 생성 Trie 생성(trie) 반복문 시작 (words 배열 순회) words배열에서 word를 가져와서 trie에 insert 반복문 종료 반복문 시작 (i부터 board 길이까지) 반복문 시작 (j부터 board[i] 길이까지) dfs 메소드 호출(board, i, j, Trie의 루트 노드, "", answer 리스트) 반복문 시작 반복문 종료 answer 반환 함수 dfs(board, i, j, node, matchingWord, answer) c = 현재 위치 (i, j) idx = c - 'a' if (c == '#' || node의 children[idx] == null) 함수 빠져나옴 matchingWord에 c를 추가 node = node의 children[idx] if (node의 isEndOfWord == true && matchingWord가 answer 리스트에 없으면) matchingWord를 answer 리스트에 추가 temp = board[i][j] board[i][j] = '#' 반복문 시작 (4번 이동, 상하좌우) i와 j를 순서대로 각각 상/하/좌/우 이동 if (i와 j가 유효범위라면) dfs 메소드 호출(board, 이동한 i, 이동한 j, node, matchingWord, answer) 반복문 종료 board[i][j] = temp |
풀이코드
class Node {
Node[] children;
boolean isEndOfWord;
public Node() {
this.children = new Node[26];
isEndOfWord = false;
}
}
class Trie {
Node root;
public Trie() {
this.root = new Node();
}
public void insert(String word) {
Node currentNode = this.root;
for (char c : word.toCharArray()) {
int idx = c - 'a';
if (currentNode.children[idx] == null) {
currentNode.children[idx] = new Node();
}
currentNode = currentNode.children[idx];
}
currentNode.isEndOfWord = true;
}
}
class Solution {
public List<String> findWords(char[][] board, String[] words) {
List<String> answer = new ArrayList<>();
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
dfs(board, i, j, trie.root, "", answer);
}
}
return answer;
}
private void dfs(char[][] board, int i, int j, Node node, String matchingWord, List<String> answer) {
char c = board[i][j];
int idx = c - 'a';
if (c == '#' || node.children[idx] == null) {
return;
}
matchingWord += c;
node = node.children[idx];
if (node.isEndOfWord && !answer.contains(matchingWord)) {
answer.add(matchingWord);
}
char temp = board[i][j];
board[i][j] = '#';
int[] dx = {-1, 1, 0, 0};
int[] dy = {0, 0, -1, 1};
for (int x = 0; x < 4; x++) {
int moveX = i + dx[x];
int moveY = j + dy[x];
if (moveX >= 0 && moveX < board.length && moveY >= 0 && moveY < board[0].length) {
dfs(board, moveX, moveY, node, matchingWord, answer);
}
}
board[i][j] = temp;
}
}코드설명
Trie자료구조와 완전탐색 문제다.
주어진 단어들을 trie자료구조로 담고, board[][] 배열을 하나씩 순회하면서 만족하는 조건이 있는지 찾는다.
Trie 자료구조를 만들기 위해 먼저 Node를 만든다.
Node는 children 배열을 가지는데 이 배열에는 26개의 문자(a~z)가 들어가고, 인덱스는 c - 'a'를 하여 0부터 25까지 저장하도록 되어있다.
다시 Trie를 만들어서 Node를 root로 맞춰주고, insert 메소드를 만든다. 이 메소드에서 words에서 word를 각각 담는다.
메인 클래스에서는 답을 찾기 위해서 배열을 DFS를 이용하여 하나씩 탐색하는데, 처음에는 trie의 root로 맞춰준다.
매개변수로는 다음과 같다.
1) 탐색할 board[][] 배열
2) i값(board 배열의 가로 인덱스)
3) j값(board 배열의 세로 인덱스)
4) node(처음에는 trie.root)
5) matchingWord(처음에는 빈 문자열)
6) answer 배열(답을 넣을 리스트)
DFS 메소드에서는 board[i][j] 배열값 1개를 가져와서 이 값이 '#'인지, 이 값을 인덱스로 Node의 children 배열이 null이 아닌지 확인한다.
만약 해당한다면 메소드를 빠져나온다.
위에 해당하지 않는다면 matchingWord에 값을 추가하고 Node를 자식Node로 바꿔준다.
Node를 자식Node로 바꿔주는 걸 처음에 해야하지만 Null이 발생할 수 있기에 먼저 위에서 처리를 하고 나중에 바꿔주는 것이다.
Node가 단어의 끝인지 확인하면서 answer리스트에 추가된 단어가 아니라면 answer리스트에 matchingWord를 넣는다.
그리고 temp 에 board[i][j] 를 넣어 저장하고, 이 값에 '#'를 넣어 갈수 없다는 표기를 한다.
이후 {-1,1,0,0} 배열과 {0,0,-1,1} 배열을 이용하여 i와 j를 상하좌우로 옮겨주는데 이동한 값이 모두 배열 내부를 만족한다면 dfs 메소드를 재귀적으로 호출한다.
상하좌우 이동이 끝나면 원래 board[i][j]에 temp값을 넣어준다.
시간복잡도 - O (n + i*j)
Trie 구조 : O(n) (n은 가장 긴 단어의 길이)
findwords메소드 : O(i*j) (최악의 경우 dfs가 배열을 전부 순회함)
공간복잡도 - O(n)
Trie 구조 : O(26 * n)
findwords메소드 : O(n)
문제를 풀며 생각한 흐름과 배운 점
계속 trie 구조를 보다보니 문제를 보자마자 이걸 사용해야겠다는 생각을 했다.
그리고 dfs 배열 탐색을 떠올렸는데 이게 생각보다 코드 구현이 쉽지 않았다.
dfs 배열에 대한 다른 문제를 공부한 뒤에 메소드를 작성할 수 있었다.
문제는 역시 런타임이 1091ms로 너무 오래 걸린다는 것이었다.
1차 개선
class Node {
Node[] children;
boolean isEndOfWord;
public Node() {
this.children = new Node[26];
isEndOfWord = false;
}
}
class Trie {
Node root;
public Trie() {
this.root = new Node();
}
public void insert(String word) {
Node currentNode = this.root;
for (char c : word.toCharArray()) {
int idx = c - 'a';
if (currentNode.children[idx] == null) {
currentNode.children[idx] = new Node();
}
currentNode = currentNode.children[idx];
}
currentNode.isEndOfWord = true;
}
}
class Solution {
public List<String> findWords(char[][] board, String[] words) {
Set<String> answer = new HashSet<>();
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
dfs(board, i, j, trie.root, "", answer);
}
}
return new ArrayList<>(answer);
}
private void dfs(char[][] board, int i, int j, Node node, String matchingWord, Set<String> answer) {
char c = board[i][j];
int idx = c - 'a';
if (c == '#' || node.children[idx] == null) {
return;
}
node = node.children[idx];
matchingWord += c;
if (node.isEndOfWord) {
answer.add(matchingWord);
}
char temp = board[i][j];
board[i][j] = '#';
int[] dx = {-1, 1, 0, 0};
int[] dy = {0, 0, -1, 1};
for (int x = 0; x < 4; x++) {
int moveX = i + dx[x];
int moveY = j + dy[x];
if (moveX >= 0 && moveX < board.length && moveY >= 0 && moveY < board[0].length) {
dfs(board, moveX, moveY, node, matchingWord, answer);
}
}
board[i][j] = temp;
}
}시간을 많이 잡아먹는 dfs는 개선해보려 했는데 그다지 큰 차이가 나지 않았다.
그래서 또 어떤 부분이 있을까 생각해보니 answer가 list여서 일일이 순회하는 데서 시간을 많이 잡아먹는 것 같았다.
자료구조를 set으로 바꾸고 그냥 add를 하여 중복제거 로직을 없앴더니 689ms 정도로 시간이 줄었다.
2차 개선
if (node.isEndOfWord) {
answer.add(matchingWord);
node.isEndOfWord = false;
}위 if문을 생각해보면 app, append가 trie에 있을때 app일때도 추가하고, append일때도 app을 추가하고 append를 추가한다.
불필요하게 app이 두번 추가되는걸 방지하기 위해서 isEndOfword를 false로 바꿔줬다.
시간은 349ms 정도로 시간이 줄었다.
다른 코드
class Solution {
public List<String> findWords(char[][] board, String[] words) {
Node root = new Node();
for (String w : words) {
Node node = root;
char[] chs = w.toCharArray();
for (char c : chs) {
if (node.next[c - 'a'] == null) {
node.next[c - 'a'] = new Node();
}
node = node.next[c - 'a'];
node.pass++;
}
node.end++;
}
List<String> res = new ArrayList<>();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
dfs(board, i, j, root, new StringBuilder(), res);
}
}
return res;
}
private int dfs(char[][] board, int i, int j, Node node, StringBuilder sb, List<String> res) {
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] == 0) {
return 0;
}
char c = board[i][j];
if (node.next[c - 'a'] == null || node.next[c - 'a'].pass == 0) {
return 0;
}
node = node.next[c - 'a'];
board[i][j] = 0;
sb.append(c);
int passed = 0;
if (node.end > 0) {
res.add(sb.toString());
node.end--;
passed = 1;
}
passed += dfs(board, i + 1, j, node, sb, res);
passed += dfs(board, i - 1, j, node, sb, res);
passed += dfs(board, i, j + 1, node, sb, res);
passed += dfs(board, i, j - 1, node, sb, res);
board[i][j] = c;
sb.deleteCharAt(sb.length() - 1);
node.pass -= passed;
return passed;
}
class Node {
int end;
int pass;
Node[] next = new Node[26];
}
}위 코드는 각 경로의 pass값을 주고 단어의 끝에 end값을 준다.
그리고 dfs로 호출할 때 단어의 끝인 end값을 만나면 end값을 -1 해주고, passed = 1 값을 가져와서 왔던 경로의 모든 구간에 pass 값을 -1 해준다.
그리고 node.next[].pass == 0 이면 바로 메소드를 빠져 나오는데, 이렇게하면 dfs 분기를 빠르게 끊을수 있다.
예를 들어 극단적인 예로 car와 careeeeeeeeeeeeeeer 라는 단어가 등록되어 있고, careeeeeeeeeeeeeeer를 이미 앞에서 찾은 경우 car 뒤에 e 부터는 굳이 찾을 필요가 없어진다.
board[][] 배열에 careeeeee가 있는 경우 careeeeee까지는 계속 확인해야 할 필요 없이, 바로 car 까지만 찾으면 끝난다.
그리고 심지어 car가 또 나오더라도 이미 구했기 때문에 구할 필요가 없어진다. 속도 측면에서 엄청난 차이가 난다.
런타임이 무려 29ms다 원래 코드의 1/30 수준이다.
완전탐색을 할 때는 탐색 제외 조건에 대해 깊이 고민해서 코드를 짜봐야겠다.
특히, 단어의 끝을 만났을때 재귀를 이용해 앞부분까지 처리하는 방법은 익혀두는게 좋을 것 같다.
정리
trie와 dfs를 문제에서 잘 적용하는 법과 dfs에서 탐색하지 않는 경우의 수를 고려할 것
'CS > 코딩테스트' 카테고리의 다른 글
| 리트코드 - 133. Clone Graph (0) | 2023.09.14 |
|---|---|
| 리트코드 - 215. Kth Largest Element in an Array (0) | 2023.09.12 |
| 리트코드 - 211. Design Add and Search Words Data Structure (0) | 2023.09.10 |
| 리트코드 - 208. Implement Trie (Prefix Tree) (0) | 2023.09.10 |
| 리트코드 - 230. Kth Smallest Element in a BST (0) | 2023.09.08 |

남에게 설명할 때 비로소 자신의 지식이 된다.
포스팅이 도움되셨다면 하트❤️ 또는 구독👍🏻 부탁드립니다!! 잘못된 정보가 있다면 댓글로 알려주세요.



