소수 판별 알고리즘 개선하기

소수 판별 알고리즘

소수는 1과 n으로만 나누어 떨어지는 정수입니다.

예를들어 1000 이하의 소수를 구하는 방법을 코드로 구현하려면 아래와 같이 일일이 1부터 n까지 나누는 계산을 하는 방법이 있습니다.

public class Main {
    public static void main(String[] args) {
        int count = 0; // 나눗셈을 시행한 횟수

        for (int n = 2; n <= 1000; n++) { // 1은 제외하고 2부터 1000까지
            int i;
            for (i = 2; i < n; i++) {
                count++;
                if (n % i == 0) {
                    break;
                }
            }
            
            if (n == i) {
                System.out.println(n);
            }
        }

        System.out.println("총 나눗셈을 수행한 횟수는: " + count + "입니다.");
    }
}

예를 들어, n=4인 경우 나누는 수인 i=2일때 count를 1회 하지만 break;문을 만나 종료하여 총 count는 1회가 됩니다.

하지만 n=5인 경우, i가 2,3,4 모두 break;문을 만나지 않기에 총 count는 3회가 됩니다.

 

이런식으로 전체 count수를 더해보면 예시 코드에서는 나눗셈을 수행한 횟수가 78022회가 됩니다.

 

그런데, n이 2 또는 3으로 나누어 떨어지지 않으면 2*2=4 로도 떨어지지 않고 2*3=6 으로도 나누어 떨어지지 않습니다.

그러므로 위 코드에서는 불필요한 연산까지 하고 있습니다.

즉, 소수가 아닌 수들로는 나눌 필요가 없고, n-1번째까지의 소수로만 나누어서 나머지가 0이 아니면 그 수는 소수인 것입니다.

시간복잡도 : O(N^2)

 

 

알고리즘 개선 첫번째

public class Main {
    public static void main(String[] args) {
        int count = 0; // 나눗셈을 시행한 횟수
        int ptr = 0;    //  찾은 소수의 갯수
        int[] prime = new int[500];   // 소수 저장 배열

        prime[ptr++] = 2;    // 2가 소수이므로 먼저 넣음

        for (int n = 3; n <= 1000; n += 2) {  // 3부터 1000까지
            int i;
            for (i = 1; i < ptr; i++) {
                count++;
                if (n % prime[i] == 0) {
                    break;
                }
            }

            if (ptr == i) {
                prime[ptr++] = n;
            }
        }
        for (int i = 0; i < ptr; i++) {
            System.out.println(prime[i]);
        }
        System.out.println("총 나눗셈을 수행한 횟수는: " + count + "입니다.");
    }
}

위 코드는 prime이라는 소수 배열을 별도로 만들어서 소수를 저장하고,

해당 배열에 있는 수로만 나누어 나머지가 0이 아닌 수들을 다시 prime 배열에 저장하는 코드입니다.

 

짝수들은 모두 2로 나누어 떨어지므로, 반복문에서는 2씩 증가되며 홀수에 대해서만 검증을 합니다.

예시코드로 나눗셈을 수행한 총 횟수는 14622회로 7만8천회에 비해 많이 개선이 되게 됩니다.

 

시간복잡도 : O(N√N)   (이유: N/2 개의 숫자에서 최대 ptr의 갯수인 √N 번 반복. 왜 소수 배열이 √N 개인지는 알고리즘 두번째에서 설명)

 

알고리즘 개선 두번째

모든 수의 약수를 생각해보면, 항상 짝을 가지고 있습니다.

예를 들어, 12인 경우 1,2,3,4,6,12를 약수로 가지고 있고, 20인 경우 1,2,4,5,10,20을 가지고 있습니다.

12는 1*12=12가 되고 2*6=12이고 3*4=12 입니다.

마찬가지로 20은 1*20=20이고, 2*10=20이고,4*5=20입니다.

 

앞부분에서 약수가 있다면, 딸려오는 나머지 약수는 반드시 존재합니다.

이를 정확히 표현하면 해당 수의 제곱근 이하에 값이 1개 있다면 이후에도 값이 1개씩 존재한다는 것입니다.

제곱근이 딱 약수인 경우 제곱근 두 번이 되죠. (예) 9인경우 3*3)

즉, 모든 수를 다 구할 필요가 없고, 제곱근 이하에서 나누어 떨어지는 소수가 없다면 그 값은 소수입니다.

public class Main {
    public static void main(String[] args) {
        int count = 0; // 나눗셈을 시행한 횟수
        int ptr = 0;    //  찾은 소수의 갯수
        int[] prime = new int[500];   // 소수 저장 배열

        prime[ptr++] = 2;    // 소수 2
        prime[ptr++] = 3;    // 소수 3 대입

        for (int n = 5; n <= 1000; n += 2) {
            boolean isPrime = false;
            for (int i = 1; prime[i] * prime[i] <= n; i++) {
                count += 2;
                if (n % prime[i] == 0) {
                    isPrime = true;
                    break;
                }
            }

            if (!isPrime) {
                prime[ptr++] = n;
                count++;
            }
        }
        for (int i = 0; i < ptr; i++) {
            System.out.println(prime[i]);
        }
        System.out.println("총 나눗셈을 수행한 횟수는: " + count + "입니다.");
    }
}

위 코드는 동일하게 prime 배열을 만들어서, 그 값인 소수의 제곱이 n보다 작을때에만 판별하도록 구성하였습니다.

count가 2인 까닭은 prime[i]*prime[i] 에서 연산 1번, n % prime[i]에서 연산 1번 해서 두 번입니다.

 

예시코드로 연산을 수행한 총 횟수는 3774회가 됩니다.

 

시간복잡도 : O(N√N)  (소수는 제곱근 이상 가질수 없으므로 √N 만큼만 계산됨. 그렇지만 연산 자체가 줄어서 처음보다 효율적임)

 

 

알고리즘 개선 세번째(에라토스테네스의 체)

소수판별 알고리즘으로 가장 많이 쓰이는 에라토스테네스의 체입니다.

2부터 n까지 모든 수를 나열하여, 소수가 아닌 수들을 소거하는 방법입니다.

 

2부터 시작하여 2를 제외한 2의 배수들을 제거합니다.

다 제거가 되면 3을 제외한 3의 배수들을 제거합니다.

4는 앞서 2의 배수로 제거가 됐으므로, 5부터 5의 배수를 제거합니다.

.

.

.

이렇게 하면 소수를 제외하고 약수를 가지는 모든 수가 제거가 됩니다.

이 알고리즘 역시 n의 제곱근까지만 판별합니다.

public class Main {
    public static void main(String[] args) {
        int n = 1000;
        boolean[] isPrime = new boolean[n + 1];
        int count = 0;

        // 배열 초기화
        for (int i = 2; i <= n; i++) {
            isPrime[i] = true;
        }

        // 에라토스테네스의 체 알고리즘
        for (int i = 2; i <= Math.sqrt(n); i++) {
            if (isPrime[i]) {
                for (int j = i * i; j <= n; j += i) {
                    isPrime[j] = false;
                    count++;
                }
            }
        }

        // 소수 출력
        for (int i = 2; i <= n; i++) {
            if (isPrime[i]) {
                System.out.println(i);
            }
        }
        System.out.println("총 나눗셈을 수행한 횟수는: " + count + "입니다.");
    }
}

이 코드는 이전과 달리 boolean타입 isPrime 배열을 만들어서 0과 1을 제외하고 true로 만들어놓고, 소거하는 방법을 사용합니다.

앞선 방법이 배열에 소수를 넣은 방법이었다면, 이번에는 n+1 개의 배열을 만들어 값을 넣고, 순차적으로 없애가는 방법입니다.

 

예시코드로 총 연산을 수행한 횟수는 1411회가 됩니다.

 

시간복잡도 : O(n*log₂(log₂N))  

 

해당 알고리즘의 시간복잡도를 확인하고자 많이 공부했으나 n + n/2 + n/3 + n/5 + ... 순의 시간복잡도가 어째서 nloglogN이 되는지는 도출해내기 어려웠습니다.

유튜브를 찾아보니 델타수열과 타우수열을 이용해 증명한 수학자분이 계시니 궁금하시면 아래를 통해 확인해보시기 바랍니다.

 

에라토스테네스 공식 도출(링크)

에라토스테네스 체의 한계

에라토스테네스의 체의 경우 n의 값이 큰 경우 만들어야 하는 배열도 크기가 커지기 때문에 메모리를 많이 잡아먹는 한계가 있습니다.

 

요약

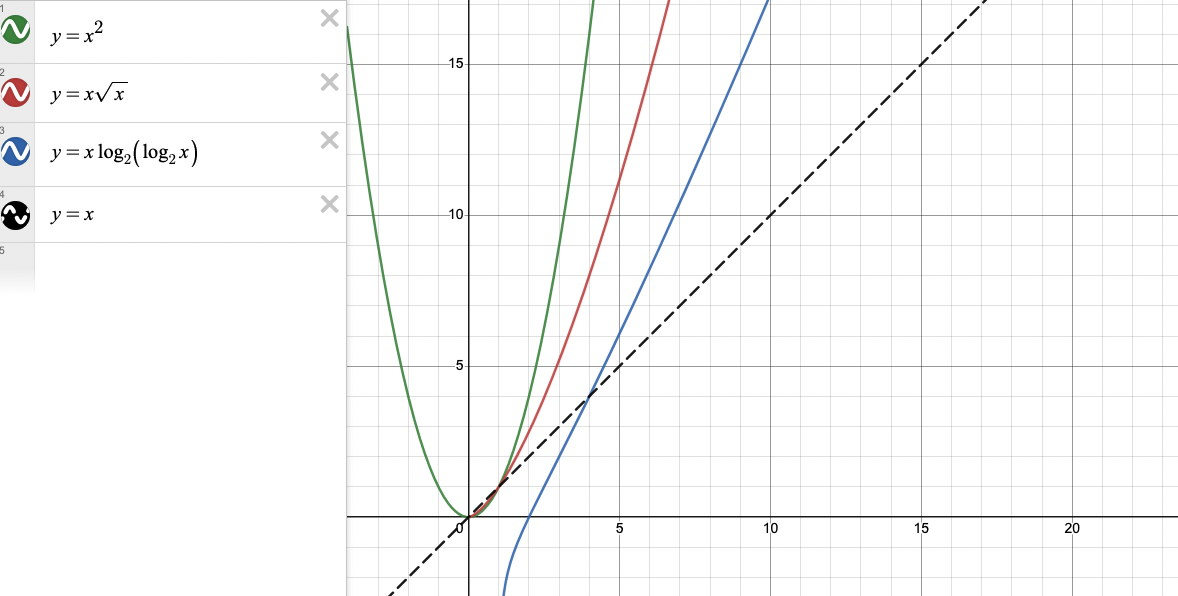
초록색 : 소수판별 알고리즘1

빨간색 : 알고리즘 1,2

파란색 : 알고리즘3(에라토스테네스의 체)

 

y=x에 가까울수록 시간이 덜 걸리는 좋은 알고리즘!

 

참고 자료

- 책) 자료구조와 함께 배우는 알고리즘 입문 자바편

- 동빈나 블로그